Удивительные факты из мира математики
 Алекс Беллос. Красота в квадрате. Как цифры отражают жизнь и жизнь отражает цифры. М., МИФ, 2019.
Алекс Беллос. Красота в квадрате. Как цифры отражают жизнь и жизнь отражает цифры. М., МИФ, 2019.
Цифры, функции и геометрические фигуры — это сплошное удовольствие. Да и сама математика — просто очень удачная шутка. Когда вы это поймете, то обязательно полюбите «царицу наук» всем сердцем. Так считает Алекс Беллос, автор книги «Красота в квадрате». Вот несколько любопытных фактов из нее, которые помогут погрузиться в безумно интересный мир чисел и графиков.
Секрет королевы
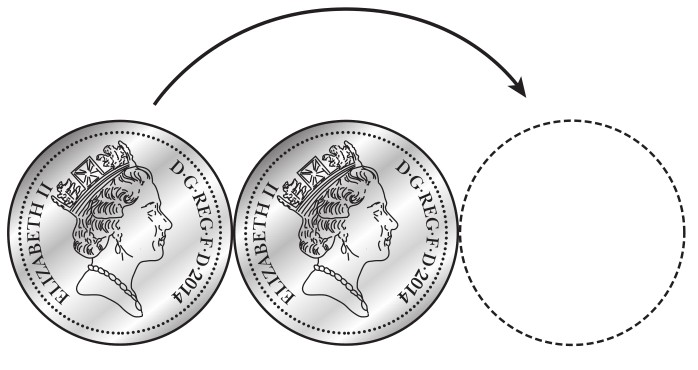
Одна из интереснейших математических головоломок сводится к перекатыванию одной монеты вокруг другой. Положите две одинаковые монеты с изображением королевы рядом друг с другом на стол, разместив их короной вверх. Прокрутите левую монету вокруг правой. В какую сторону будет направлена корона, когда монета окажется с правой стороны?
Вы предположите, что монета окажется в перевернутом положении, поскольку она прошла только половину пути вокруг неподвижной монеты? Это ошибка. Королева делает полный оборот, что на первый взгляд противоречит здравому смыслу. Дело в том, что монета вращается вокруг себя и вокруг другой монеты. Движение происходит в двух независимых направлениях. На каждый градус перемещения левой монеты вокруг правой приходится два градуса ее вращения вокруг себя.
Почему четное число не может быть мистическим
Шумеры придумывали для чисел названия, пользуясь имеющимися в их языке словами. Например, для обозначения единицы употреблялось слово ges («геш»), второе значение которого — мужчина или фаллос. Двойка обозначалась словом min («мин»), также символизирующим женское начало. Возможно, это подчеркивало то, что мужчина занимает доминирующее положение, а женщина — лишь дополнение к нему, или характеризовало мужской половой член и женскую грудь.
Греческий мыслитель Пифагор, живший в VI веке до нашей эры, провозгласил нечетные числа мужскими, а четные — женскими, тем самым подтвердив отмеченную шумерами ассоциативную связь между единицей и мужчиной, а также двойкой и женщиной. Он утверждал, что нежелание делиться на два — это признак силы, тогда как склонность к такому делению — признак слабости. В христианстве это нашло отражение в мифе о сотворении мира: Адама Бог создал первым, а Еву — второй.
Эти предрассудки сохранились до наших дней. Мистическими по-прежнему считаются только нечетные числа.
Фокус с цифрами
Если подсчитать частотность первых цифр во всех числах, которые вы найдете на первой полосе любой газеты, то можно заметить интересную закономерность. Вы увидите, что числа, начинающиеся с цифры 1, встречаются чаще всего; затем следуют числа, первая цифра которых 2, потом 3 — и так далее до цифры 9, которая используется в начале чисел реже всего. Это действительно невероятно. Попробуйте сделать это сами!
В 1938 году, физик из General Electric Фрэнк Бенфорд открыл феномен первой цифры, обратив внимание на потрепанность страниц в книгах с таблицами логарифмов. Он изучил распределение первых цифр исходя из таких данных, как население городов США, адреса первых нескольких сотен людей из биографического справочника американских ученых American Men of Science, атомный вес химических элементов, площадь бассейна рек и статистика бейсбольных матчей. В большинстве случаев результаты были близки к ожидаемому распределению.
Метод анализа чисел на предмет их соответствия закону Бенфорда все чаще используется для выявления манипуляций с данными, причем не только в контексте финансовых махинаций, но и во всех тех случаях, к которым этот закон применим.
В 2006 году Скотт де Марчи и Джеймс Гамильтон из Университета Дьюка написали, что предоставленные промышленными предприятиями сведения об уровне выброса свинца и азотной кислоты не удовлетворяют закону Бенфорда, а это говорит о вероятности искажения информации.
На основании закона Бенфорда политолог Мичиганского университета Уолтер Мибейн заявил о возможной фальсификации результатов президентских выборов в Иране. Ученые используют закон Бенфорда и в качестве инструмента диагностики. Так, во время землетрясений верхние и нижние значения показаний сейсмографа подчиняются данному закону.
Как продать дом подороже
Психолог Корнельского университета Маной Томас утверждает, что из-за чувства дискомфорта, порождаемого большими некруглыми числами, их значение кажется нам меньше, чем оно есть в действительности: «Мы склонны полагать, что малые числа более точны, поэтому, видя точное большое число, инстинктивно предполагаем, что оно меньше, чем на самом деле». В итоге, по мнению Маноя Томаса, мы платим за дорогой продукт больше, если его цена представлена некруглым числом.
Во время одного из экспериментов Томас дал испытуемым фотографии нескольких домов, где были также указаны их цены, в произвольном порядке представленные либо круглым числом (скажем, 390 000 долларов), либо чуть большим точным числом (например, 391 534 доллара).
Когда респондентов спросили, какую цену они считают выше, а какую ниже, они в среднем оценили точные цены как более низкие, хотя на самом деле все было наоборот. Совет тем, кто собирается продавать дом: если хотите выручить за него больше денег, его цена не должна заканчиваться нулем.
В мире простых чисел
Джерри Ньюпорт — бывший таксист из города Тусон, страдающий синдромом Аспергера, психическим расстройством, при котором человек испытывает трудности в межличностном общении, но обладает уникальными талантами. Когда Джерри видит большое число, он сразу же делит его на простые числа — 2, 3, 5, 7, 11… то есть числа, которые делятся только на себя и единицу.
«Я обращаю внимание только на числа, в которых больше четырех цифр. если же их меньше, это как раздавленное на дороге животное. Да, именно так! — возмущенно заявляет он. — Ну же, покажите мне что-нибудь новенькое!»
Иногда Джерри не удается разложить большое число на простые множители, а это означает, что данное число само является простым.
«Когда встречаешь новое простое число, это как будто смотришь на камни и находишь среди них что-то необычное. Нечто вроде бриллианта, который можно взять домой и положить на полку, — объясняет Джерри. — Новое простое число — это как новый друг».
Парадокс бесконечности
Философ Зенон предостерегал против использования такого понятия, как бесконечность, в серии парадоксов. В самом знаменитом из них, «Ахиллес и черепаха», демонстрировалось, что сложение бесконечного количества величин приводит к абсурдному результату.
Представьте себе, говорил Зенон, что Ахиллес пытается догнать черепаху. Когда атлет достигнет того места, где она была, когда он начал свой бег, черепаха проползет немного дальше. Когда он доберется до второй позиции, черепаха снова продвинется дальше. Ахиллес может продолжать свой бег сколько угодно, но каждый раз, когда он будет достигать того места, где находилась черепаха, она уже будет немного впереди.
Зенон утверждал, что если рассматривать движение как бесконечное количество рывков на протяжении бесконечного количества интервалов, то быстроногий Ахиллес никогда не догонит неповоротливую черепаху. Древние греки так и не смогли развязать логические узлы Зенона, поэтому долго математики избегали концепции бесконечности в своей работе.
По материалам книги «Красота в квадрате».
